1) Transversal Line
2) Equal Alternate Interior Angles
3) Alternate Exterior Angles
4) Corresponding Angles
Understanding alternate interior angles along with alternate exterior angles, really starts with learning about what is known as a Transversal Line.
Transversal Line
If we have two separate straight lines, they can both be crossed by a third straight line, which is called a “Transversal” line.
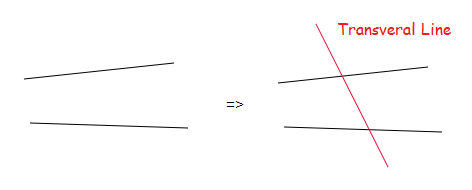
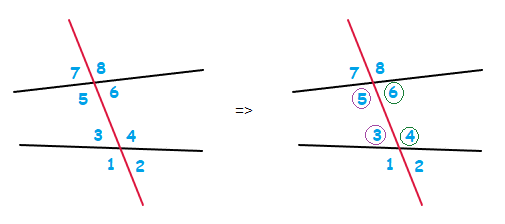
This transversal line crossing through 2 straight lines, creates 8 angles.
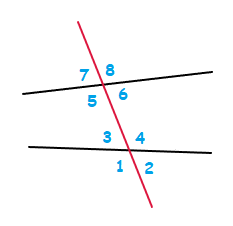
In the image above, angles 3, 4, 5 and 6 are the INTERIOR angles.
From these interior angles, angles 4 and 5 are ALTERNATE INTERIOR angles.
The angles 3 and 6 are also ALTERNATE INTERIOR angles.
These are angles that are INTERIOR, and also on different/alternative sides of the red transversal line that is present.
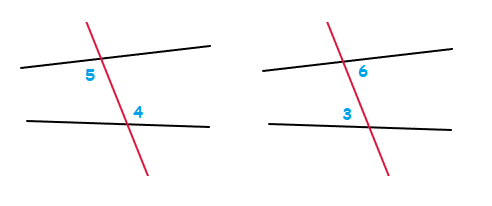
Equal Alternate Interior Angles
When a Transversal line crosses through 2 straight parallel lines, the interior alternate angles that are created will be equal alternate interior angles.
Angle 4 = Angle 5 , Angle 3 = Angle 6
Consecutive Interior Angles
Angles 4 and 6 together in this situation are known as “consecutive interior angles”.
As are angles 3 and 5.
They are interior angles, both on the same side of the Transversal line as one another. Thus they are called “consecutive”.
When a Transversal line crosses parallel lines, the consecutive interior angles add up to 180°.
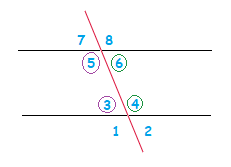
Angle 3 + Angle 5 = 180° , Angle 4 + Angle 6 = 180°
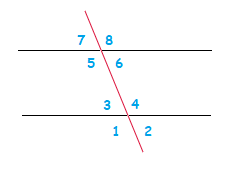
Alternate Exterior Angles
It’s the case that Exterior angles are also created when a transversal line crosses 2 separate straight lines.
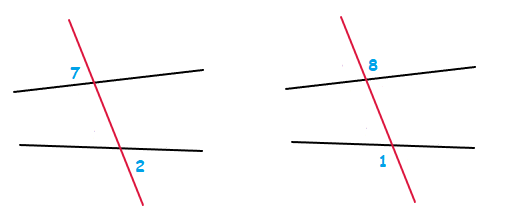
Similar to before, angles 1, 2, 7 and 8 are EXTERIOR angles.
The angles 2 and 7 are ALTERNATE angles, and the angles 1 and 8 are also ALTERNATE.
Also like with the case of interior angles, the above exterior angles are equal when a transversal line crosses 2 straight parallel lines.
Example
1.1
For the following triangle, what size are the inside angles A, B and C?
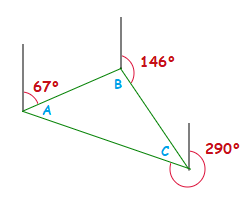
Solution
First look towards angles B and C.
We can draw in some extra vertical lines that aren’t part of the triangle itself, these lines will be helpful to establish the sizes of angles B and C.
The vertically opposite angles page has some more information, along with the information on this page, that can help direct how we can fill in some extra angle sizes around angles B and C.
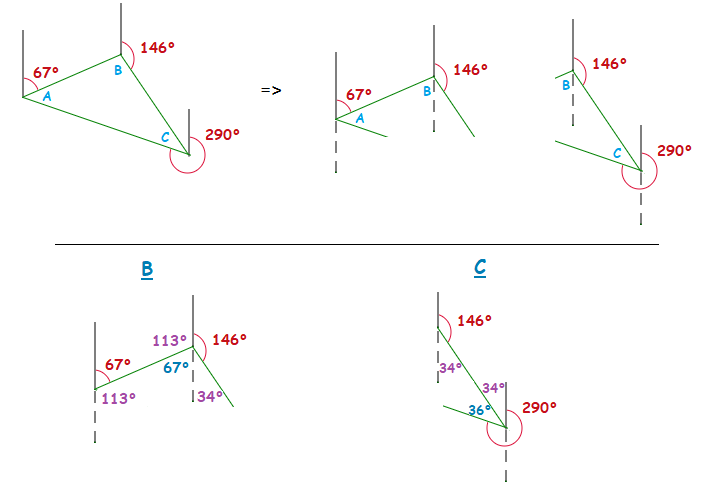
Now as there is 180° in a triangle, the size of angle A can easily be worked out by subtracting angles B and C from 180°.
A = 180° − 101° − 36° = 43°
Corresponding Angles
Corresponding angles are a mix of both an interior angle, and an exterior angle.
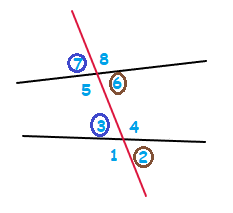
In the above image, angles 3 and 7 together are corresponding angles, as are angles 2 and 6.
But also, angles 4 and 8 together and angles 1 and 5 together are corresponding angles too.
When the lines being crossed by the Transversal line are parallel, then the corresponding angles are equal to each other in size.
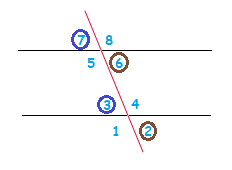
Angle 1 = Angle 5 , Angle 2 = Angle 6
Angle 3 = Angle 7 , Angle 4 = Angle 8