The 3 angles that form inside a standard triangle always add up to a total of 180°.
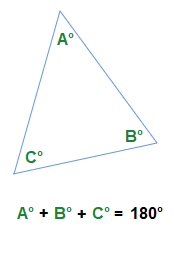
We can try this out for ourselves anytime with angles in triangles.
Simply draw any basic triangle, then use an appropriate tool to measure the inside angles, and the angles will add up to 180°.
Example
1.1
What size is the angle a?
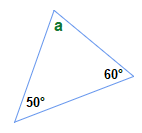
Solution
All 3 angles added up together are 180°.
a = 180° − 60° − 50° = 180° − 110° = 70°When we know the size of 2 of the angles present in a standard triangle, we can establish the size of the third angle when we wish.
As it turns out, the largest sized angle inside a triangle is the angle that is opposite the longest side.
With the smallest angle being the angle that sits opposite the shortest side.
Interior Angles in Common Shapes
Square or Rectangle
A square or rectangle, has 4 right angles inside the overall shape.
All of these right angles together add up to 360°.
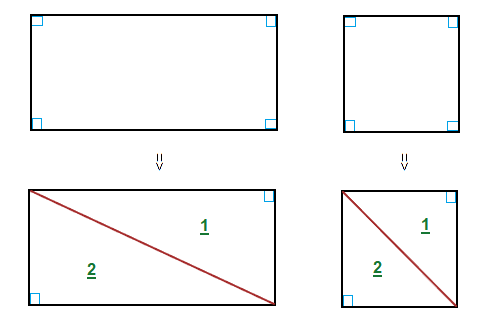
As can be viewed, a square or rectangle is made up of 2 smaller right angle triangles.
So 2 × 180° = 360°.It can also be seen that each of the angles inside a square or rectangle is the same size, with each angle being 90° in size.
360° ÷ 4 = 90°Angles in Polygon Shapes
So we have learned about the angles in triangles and squares/rectangles.
But what about some other shapes, shapes that can have an even greater number of sides.
Are the angles that can be found inside other shapes following a similar pattern?
Well, provided the flat 2D shape involved is a regular polygon, where we have all sides the same length.
Then it’s the case that all inside angles will also happen to be the same size as each other.
Such as in a square where each inside angle is 90°
There is a useful formula that can help tell us how many degrees are inside such a regular polygon shape.
Angles in Triangles:
Polygon Interior Angles Formula
For a regular polygon with number of sides n.
The angles inside the shape add up to the following total degrees. ( n − 2 ) × 180°.
Thus the size of one interior angle is given by. \bf{\frac{(n \space {\text{--}} \space 2) \space \times \space 180\degree}{n}}
Examples
2.1
Pentagon.
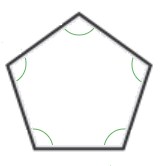
A regular Pentagon has 5 sides, n = 5
( n − 2 ) × 180°
=> ( 5 − 2 ) × 180°
=> 3 × 180° = 540°
The interior angles of a regular Pentagon add up to 540°.
As there are 5 equal angles inside the Pentagon, we can obtain the size of each angle.
Interior Angle = \bf{\frac{540\degree}{5}} = 108°
Each separate angle inside a regular Pentagon is 108° in size.
2.2
Hexagon.
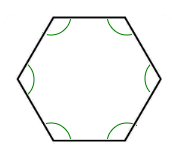
A regular Hexagon has 6 sides, n = 6
( n − 2 ) × 180°
=> ( 6 − 2 ) × 180°
=> 4 × 180° = 720°
The angles inside a regular Hexagon add up to 720°.
Interior Angle = \bf{\frac{720\degree}{6}} = 120°Each separate angle inside the Hexagon is 120° in size.
2.3
Heptagon.
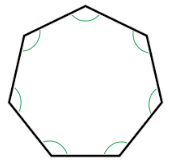
A regular Hexagon has 7 sides, n = 7
( n − 2 ) × 180°
=> ( 7 − 2 ) × 180°
=> 5 × 180° = 900°
The angles inside a regular Heptagon add up to 900°.
Interior Angle = \bf{\frac{900\degree}{7}} = 128.57…°Each separate angle inside the Hepagon is 128.57…° in size.
This approach can be used for shapes with greater numbers of sides also.
Also a pattern no note is that each time we add on another side to a flat 2D regular polygon shape, the size of all the internal angles together increases by 180°.