This page will look to give a detailed and clear area measure introduction.
2D Area Intro, Rectangle/Square
When in 2 dimensions, area is the measure of the amount of space there is on a flat surface, enclosed within a certain boundary.Probably the simplest shape to look at when thinking about 2D area measure is a square or a rectangle shape.
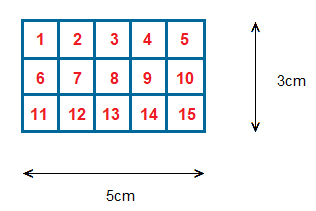
The rectangle shown above, is 3cm high, and also 5cm wide.
It is made up of 15 smaller squares, each of which is 1cm high, and 1cm wide.
Rather than counting all of the smaller squares though, when we need to work out the area of a standard square or rectangle.
We can do the sum of multiplying the width by the height.
So for the rectangle shown above.
5 × 3 = 15
The total area of the rectangle is 15 square centimetres.
Area Measure Introduction, Dimensions
It’s important to make sure that the dimensions are the same on all sides of the shape.
For example a rectangle could be:
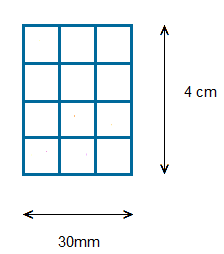
For the total area in square centimetres, we would have to convert the width from millimetres to centimetres.
30 millimetres is 3 centimetres.
Area = 4 × 3 = 12 , 12 square centimetres
Notation
The correct notation for area values is important to learn and remember.Instead of writing out the words square centimetres, a shorter notation of cm2 is usually used.
Similarly if an area measurement in metres, m2 is used.
This is the relevant unit being measured, to the power of 2.
Example

1.1
What is the area in square metres of a rectangular garden that is 10 metres wide, and 600 centimetres long.
Solution
600 centimetres is 6 metres. 600cm = 6m
10 × 6 = 60 , The area of the rectangular garden is 60m2.
Area Units
Like in the case of length, it’s important to note in an area measure introduction that area is also measured in a range of different units.Above we’ve seen centimetres and metres, but there are other values of area measure that can be encountered.
The size of rooms in building plans for example are often measured in square feet, ft2.
Large land areas such as countries are usually measured and displayed in square miles, mi2, or square kilometres, km2.
In each case though, it’s the same principle as the earlier example on this page.
How many smaller squares are there that cover a larger surface area.