The area of an ellipse formula, follows on from learning how to work out the area of a circle.
If we consider the overall shape, an ellipse is generally quite similar to a standard circle.
An ellipse will often have the appearance of a stretched circle, or a compressed circle, depending on ones point of view.
Axis of an Ellipse
It’s the case that an ellipse happens to be symmetrical in shape, on both a major axis and a minor axis.The major axis is the larger diameter, and the minor axis is the smaller diameter of the ellipse.
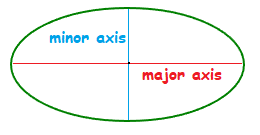
The major and minor axis can be both be cut in half, which results in what is called the semi major axis, and a semi minor axis.
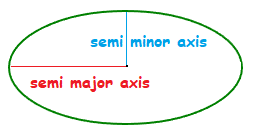
Area of an Ellipse Formula
For a circle, the distance from the central point to any part of the outer edge, is always the same size, this length is called the radius of the circle.
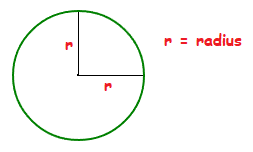
π × r2 or π × r × r
Using Area of Circle for an Ellipse:
With an ellipse, the distance from the central point to the outer edge is not the same all the way around like in a circle.But as mentioned, the ellipse shape is symmetrical.
With both of the semi major axis having the same length, and both of the semi minor axis also having the same length.
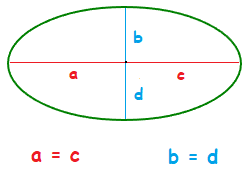
So in a similar way to how the area of a circle is established by, π × r × r.
The area of an ellipse can be established by, π × a × b.
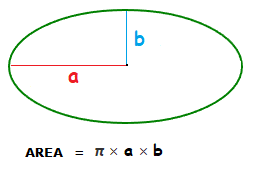
This is the area of an ellipse formula, that can be used to find the area of an ellipse.
Provided that you know the length of the semi minor axis and the semi major axis.
Examples
1.1
What is the area of the following ellipse.
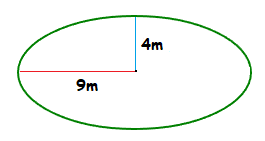
Solution
Area = π × 9 × 4 = 113.1 ( to 2 decimal places )
The area of the ellipse is 113.1m2.
1.2
If the area of the following ellipse is 65.97m2.
Roughly what length is the major axis?
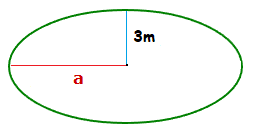
Solution
65.97 = π × 3 × a ( ÷ π × 3 BOTH SIDES )
\frac{\bf{65.97}}{\pi \space \times \space {\bf{3}}} = a
6.999… = a
The semi major axis a is roughly 7m in length.