Coterminal angles in Math are angles that share the same initial and terminal side between them.
So prior to fully concentrating on coterminal angles, it helps to fully understand about the initial side and the terminal side of an angle.
Initial and Terminal Sides of Angles
A flat 2D angle formed between 2 straight lines will have one initial side, and one terminal side.
The initial side is the beginning side for the angle measurement,
and the terminal side is the ending side for the angle measurement.
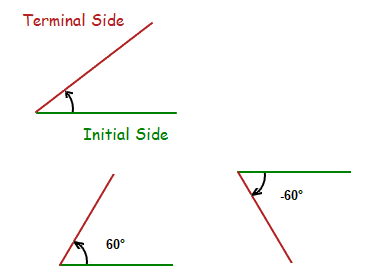
On a standard 2D Cartesian Coordinate axis, the initial side for a given angle is very often the line in the position of the positive x-axis.
With the end point/vertex of the angle being at the point (0,0).
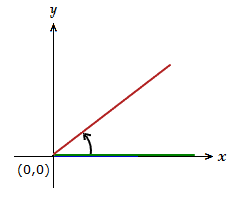
The angle above is measured starting from the blue line on the x-axis that is the initial side, and ending at the green line that is the terminal side.
Coterminal Angles in Math
As mentioned at the beginning of the page, coterminal angles in Math are angles that happen to share the same initial side and terminal side.
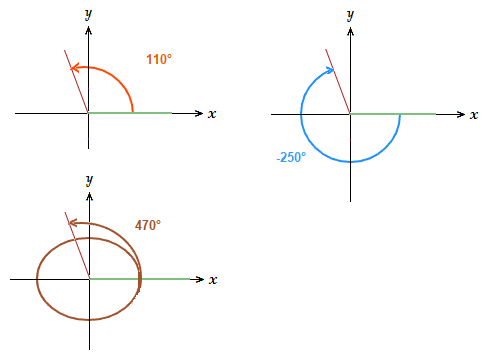
A = 110° , B = –250° , C = 470°
Each angle A, B and C above, despite being different sizes,
begin at the same line/side as one another, and also end at the same line/side as one another.
So they are angles that are coterminal with each other.
Relationship between Coterminal Angles
The relationship between these coterminal angles is that they differ in size by 360°. 110° − 360° = -250° , 110° + 360° = 470°So anytime you wish to find an angle that is coterminal to another angle, you just add or subtract 360°.
For example with an angle of size 80°.80° + 360° = 440° , 80° − 360° = –280°
–280° , 80° and 440° are angles that are all coterminal with each other.
Really there are in fact an infinite number of potential coterminal angles that can share the same initial and terminal sides.
As we could go around a circle by 360° in either a positive or a negative direction as many times as we wished, to many coterminal angles.
Coterminal Angles and Radians
Things also work exactly the same way when dealing with radian measurement of angles as they do with degrees.
But in this situation, it is 2π that is added or subtracted to an initial angle, rather than 360°.
Due to the fact that with radian measure, 2π = 360°.
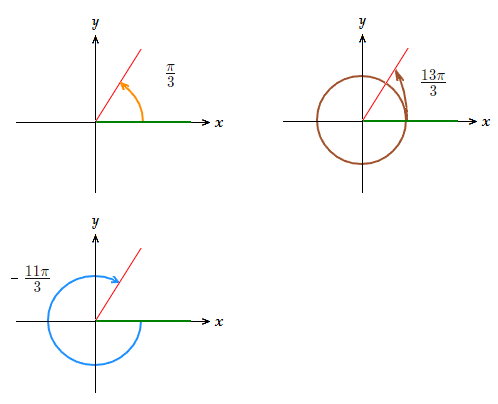
The angles above are coterminal in radian measurement. \boldsymbol{\frac{\pi}{3}} , \boldsymbol{\frac{13\pi}{3}} , –\boldsymbol{\frac{11\pi}{3}}
\boldsymbol{\frac{\pi}{3}} + 2π = \boldsymbol{\frac{13\pi}{3}} , \boldsymbol{\frac{\pi}{3}} − 2π = –\boldsymbol{\frac{11\pi}{3}}
Examples
1.1
Consider an initial angle of θ = 160°.
Find one positive coterminal angle and one negative coterminal angle.
Solution
We only need to do θ + 360° AND θ − 360°.
This will provide one positive and one negative coterminal angle with 160°.
160° + 360° = 520°
160° − 360° = –200°
Angles 520° and –200° are coterminal with 160°.
1.2
With an initial angle of θ = \boldsymbol{\frac{2\pi}{5}},
find one positive coterminal angle and one negative coterminal angle.
Solution
As θ here is in radian measure.
We will look to perform θ + 2π AND θ − 2π
That will give us a positive and a negative coterminal angle with \boldsymbol{\frac{2\pi}{5}}.
\boldsymbol{\frac{2\pi}{5}} + 2π = \boldsymbol{\frac{2\pi}{5}} + \bf{\frac{10\pi}{5}} = \boldsymbol{\frac{12\pi}{5}}
\boldsymbol{\frac{2\pi}{5}} − 2π = \boldsymbol{\frac{2\pi}{5}} − \bf{\frac{10\pi}{5}} = –\boldsymbol{\frac{8\pi}{5}}
Angles \boldsymbol{\frac{12\pi}{5}} and –\boldsymbol{\frac{8\pi}{5}} are coterminal with \boldsymbol{\frac{2\pi}{5}}.
1.3
With an initial angle of θ = 50°.
Obtain two negative coterminal angles.
Solution
As we want two negative coterminal angles, we will subtract 360° twice from 50°.
Subtracting 360° twice will result in two negative angles that are coterminal.
50° − 360° = –310°
–50° − 360° − 360° = –670°
–310° and –670° are coterminal with 50°