Skip to content

Dividing Fractions
Dividing Fractions with Different Denominators



When dealing with dividing fractions sums, the basic idea is the same as when we deal with dividing whole numbers.


If you divide  12  by  3,  you find out how many  3‘s  there are in  12.       12 ÷ 3  =  4

Likewise if you were to divide   \frac{5}{6}   by   \frac{1}{4}, 

you find out how many   \frac{1}{4}‘s   there are in   \frac{5}{6}.


Fortunately, fractions division shares similarities to fractions multiplication in many cases.




Dividing Fractions with the Same Denominator

The simplest case for dividing fractions is when we want to divide fractions with the same denominator.

When this is the case, the result of the division is a fraction.

A fraction containing the numerators of the fractions in the division sum.

The numerator of the first fraction is the numerator of the new fraction.
While the numerator of the second fraction is now the denominator of the new fraction.


Examples




1.1

\bf{\frac{3}{5}} ÷ \bf{\frac{2}{5}}   =   \bf{\frac{3}{2}}



1.2

–\bf{\frac{5}{4}} ÷ \bf{\frac{7}{4}}   =   –\bf{\frac{5}{7}}







Dividing Fractions with Different Denominators

When dividing fractions with different denominators, we want to flip the dividing fraction upside down, and then multiply both fractions together.


Examples




2.1

\bf{\frac{1}{2}} ÷ \bf{\frac{3}{5}}   =   \bf{\frac{1}{2}} × \bf{\frac{5}{3}}   =   \bf{\frac{5}{6}}


2.2

\bf{\frac{7}{10}} ÷ \bf{\frac{12}{15}}   =   \bf{\frac{7}{10}} × \bf{\frac{15}{12}}   =   \bf{\frac{105}{120}}   =   \bf{\frac{7}{8}}


2.3

\bf{\frac{9}{5}} ÷ \bf{\frac{3}{4}}   =   \bf{\frac{9}{5}} × \bf{\frac{4}{3}}   =   \bf{\frac{36}{15}}   =   \bf{\frac{12}{5}}


2.4

3 ÷ \bf{\frac{1}{4}}   =   \bf{\frac{3}{1}} ÷ \bf{\frac{1}{4}}     =   \bf{\frac{3}{1}} × \bf{\frac{4}{1}}   =   \bf{\frac{12}{1}}   =   12


2.5

5 ÷ \bf{\frac{4}{3}}   =   \bf{\frac{5}{1}} ÷ \bf{\frac{3}{4}}     =   \bf{\frac{5}{1}} × \bf{\frac{3}{4}}   =   \bf{\frac{15}{4}}


2.6

\bf{\frac{4}{3}} ÷ 5   =   \bf{\frac{4}{3}} ÷ \bf{\frac{5}{1}}     =   \bf{\frac{4}{3}} × \bf{\frac{1}{5}}   =   \bf{\frac{4}{15}}




Summary

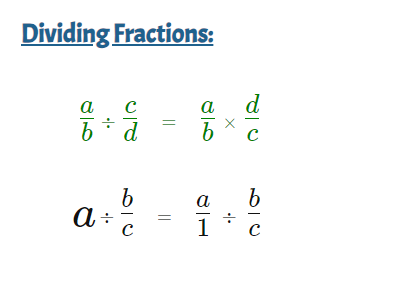
General case for dividing fractions.


Dividing Fractions, Mixed Fractions


When division with mixed fractions is involved, we will want to convert the mixed fraction into improper fraction form first to make things easier.
Information on how to convert mixed fractions to standard fractions can be seen here.



Examples




3.1

2\bf{\frac{1}{4}}  ÷  1\bf{\frac{1}{3}}   =   \bf{\frac{9}{4}} ÷ \bf{\frac{4}{3}}   =   \bf{\frac{9}{4}} × \bf{\frac{3}{4}}   =   \bf{\frac{27}{16}}   =   1\bf{\frac{11}{16}}


3.2

3\bf{\frac{4}{5}}  ÷  5\bf{\frac{1}{2}}   =   \bf{\frac{19}{5}} ÷ \bf{\frac{11}{2}}   =   \bf{\frac{19}{5}} × \bf{\frac{2}{11}}   =   \bf{\frac{38}{55}}







Complex Fractions

Knowing the properties of fraction division can be particularly handy when we deal with what are known as “complex fractions”.

Complex fractions are fractions where one of either the numerator on top, or the denominator on the bottom, are also a fraction themselves.
Though sometimes both the numerator and the denominator can be fractions at the same time.

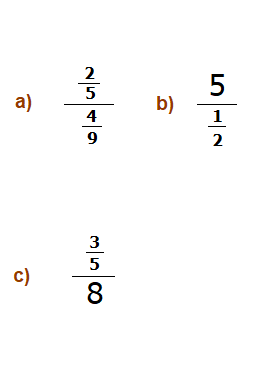
The following are examples of a complex fraction.

Sums with Complex Fractions:

Sums involving complex fractions usually involve at some point, simplifying or converting the complex fraction to a simpler fraction, or even at times a whole number.


Examples



4.1

Simplify the complex fraction   \bf{\frac{6}{\tiny\frac{1}{4}}}   as much as possible.

Solution

This fraction can be looked at as   6 ÷ \bf{\frac{1}{4}}.

Which is the same as   \bf{\frac{6}{1}} ÷ \bf{\frac{1}{4}}.

Now:   \bf{\frac{6}{1}} ÷ \bf{\frac{1}{4}}    =    \bf{\frac{6}{1}} × \bf{\frac{4}{1}}    =    \bf{\frac{24}{1}}   =   24



4.2

Convert   \bf{\frac{14}{\tiny\frac{4}{3}}}   to a simpler fraction.

Solution

Again thinking of   \bf{\frac{14}{1}} ÷ \bf{\frac{4}{3}}.

\bf{\frac{14}{1}} ÷ \bf{\frac{4}{3}}    =    \bf{\frac{14}{1}} × \bf{\frac{3}{4}}    =    \bf{\frac{42}{4}}    =    \bf{\frac{21}{2}}



4.3

Convert   \bf{\frac{\tiny\frac{3}{4}}{5}}   to a simpler fraction.

Solution

\bf{\frac{3}{4}} ÷ 5    =    \bf{\frac{3}{4}} ÷ \bf{\frac{5}{1}},

\bf{\frac{3}{4}} ÷ \bf{\frac{5}{1}}    =    \bf{\frac{3}{4}} × \bf{\frac{1}{5}}    =    \bf{\frac{3}{20}}



4.4

Convert   \bf{\frac{\tiny\frac{5}{6}}{\tiny\frac{4}{9}}}   to a simpler fraction.

Solution

\bf{\frac{5}{6}} ÷ \bf{\frac{4}{9}}    =    \bf{\frac{5}{6}} × \bf{\frac{9}{4}}    =    \bf{\frac{45}{24}}







  1. Home
    2.  ›
  2. Fractions and Decimals
    3. › Division of Fractions


Return to TOP of page