Division sums in their simplest form, generally amount to dividing or separating a bigger group, into a smaller group or groups.
More Mathematically speaking, dividing a greater number into lesser numbers.
Now one can divide a smaller number by a larger number as well when required.
However this division sums introduction page just focuses on dividing a larger number by a smaller number to introduce the idea.
Along with looking at division and remainders when they occur.
Symbol for Division
The symbol for division is ÷.
Thus 16 divided by 8,
looks like 16 ÷ 8.
Although it is the case that often division sums can be written like a fraction in the form:
\frac{16}{8}
The top number is the number being divided by the lower number.
This top number is called the NUMERATOR.
The lower number is called the DENOMINATOR. \frac{NUMERATOR}{DENOMINATOR}
Examples
1.1
6 ÷ 3 =
Thinking about this division, let’s say that we have 6 tennis balls.
Dividing by 3, means that we want to split the 6 tennis balls into 3 : groups.
The answer to the sum, is what size the 3 groups being split into are.
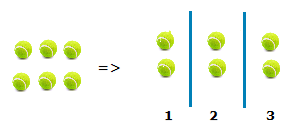
The initial group of 6 tennis balls, divided into 3 groups of tennis balls, gives a result of size 2.
So we have, 6 ÷ 3 = 2.
1.2
8 ÷ 2 =
If we again think in terms of tennis balls.
Dividing up a group of 8 into 2 groups.
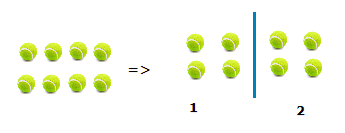
We can see that 2 groups of 4 are made.
So, 8 ÷ 2 = 4
Division by 1
Division by 1 always has the same result when carried out.
If we had, 7 ÷ 1 =
We will be splitting a group of 7 into 1 group.
But division by 1 really means not splitting or dividing up at all.

There already was one group of 7.
Thus division of one group of 7 into one group, simply results in the same group/number that was already there.
A number divided by 1 , will just result in the same number.
So, 7 ÷ 1 = 5 , 2 ÷ 1 = 2 , 10 ÷ 1 = 10 etc.
Division and Remainders
There are times when a division of a larger number into a smaller number doesn’t result in an equal division, when we have division and remainders.
We could have, 9 ÷ 2 =
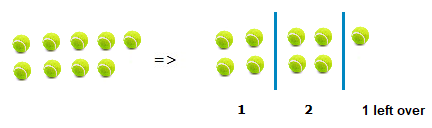
It turns out that a group of 9 does divide into 2 groups of 4, but there does end up being 1 tennis ball left over, 1 tennis ball remaining.
So, 9 ÷ 2 = 4 remainder 1.
A result such as this which includes a remainder, is often denoted as 3r1.
We can also look at, 7 ÷ 5 =.
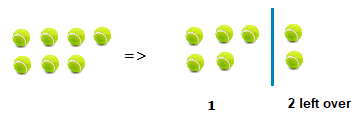
7 ÷ 5 = 1r2
Division with Zero
Another important case to show in a division sums introduction is division when 0 is involved.
Firstly, the case of dividing the number 0.
Say we had the following. 0 ÷ 4 =
If we have 0 tennis balls, then there is no group to divide or split up.
So there is still no group at all after any division.
Which means that zero divided by a non zero number results in just zero.
0 ÷ 1 = 0 , 0 ÷ 4 = 0 , 0 ÷ 5 = 0 etc.
There is also the case of dividing by 0.
We could have 4 ÷ 0 =
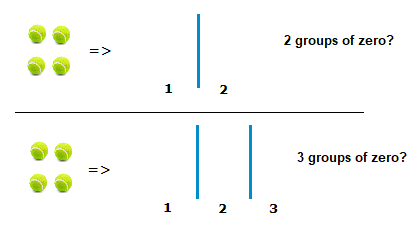
There isn’t really an answer we can come up with for how many groups of zero can be made from a group of 4.
As such, when a number is divided by 0, the answer is classed as undefined.
- Home ›
- Arithmetic/Numbers › Division Sums Introduction