This Factoring in Algebra section looks to introduce how to approach factoring algebraic expressions, similar to how we can factor numbers.
Factoring can also be referred to as factorization.
What is a Factor Recap
When it comes to numbers, a factor is a number that divides another number exactly.
For example with the number 8.
The factors are 1 , 2 , 4 and 8 itself.
As 8 also divides 8, exactly once.
As seen, 8 can be factored.
The factors 2 and 4 multiplied together as a product, give 8.
Factoring Algebraic Expressions
It’s not only numbers that can be factored with factoring in Algebra.
Many equations and expressions when in appropriate form, can also be factored when necessary. This page will show how to approach factoring algebraic expressions.
Removing Brackets Reverse
If you’re familiar with the process of removing or expanding brackets, factoring involving equations and expressions is in many cases the opposite process.
You’re not multiplying terms out, instead you’re attempting to go the other way. In order to establish which terms that when multiplied out together, give you a specific equation or expression.
For example we can consider 2x + 6. A simple expression that can be factored.
2x and 6 have a common factor of 2.
So the expression can be rewritten as, 2(x + 3)
2 × (x + 3) = 2x + 6
2 and (x + 3) are factors of 2x + 6.
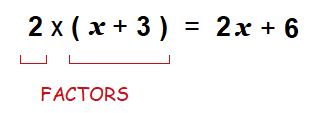
Examples
1.1
3x + 15 = 3(x + 5)
1.2
4x2 + 24x = 4(x2 + 6x) = 4x(x + 6)
Zero Factor Property
Something that can sometimes be handy for dealing with certain proofs is the zero factor property.
If a × b = 0, then either a = 0 or/and b = 0.