It’s important to know in Mathematics how to manipulate expressions that involve brackets.
Removing brackets in simpler cases, often comes down to multiplying brackets out, with an approach known as the FOIL method.
This page will show some FOIL method examples with answers.
Removing brackets can sometimes be referred to as expanding brackets.
4(x + 1) = 4x + 1
This comes about from multiplying first 4 by x, and then 4 by 1.
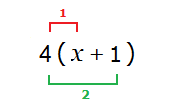
Generally:
x( y + z ) = xy + xz and x( y − z ) = xy − xz
Examples
1.1
2( x + 7 ) = 2x + 14
1.2
3( 2x − 4 ) = 6x − 12
1.3
x( y + 5 ) = xy + 5x
1.4
-2b( 6 − b ) = -12b + 2b2
1.5
p( q + r ) = pq + pr
FOIL Method Examples with Answers
Sometimes it’s required to expand or multiply out 2 separate expressions that both involve 2 terms.
There’s a bit more multiplication to be done than in the smaller examples above, but the general approach is very similar.
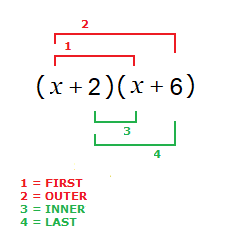
There are 4 multiplications to do, then usually a little bit of addition or subtraction.
This method is sometimes referred to as the FOIL Method.
Meaning First , Outer , Inner , Last,
in order of the operations, as can be seen in the image above.
(x + c)(x + d) = x2 + xd + xc + cd = x2 + (c + d)x + cd
Examples
2.1
(x − 3)(x + 2) = x2 + 2x − 3x − 6 = x2 − x − 6
2.2
(2x + 1)(x + 4) = 2x2 + 8x + x + 4 = 2x2 + 9x + 4
2.3
(2x − 1)(2x + 1) = 4x2 + 2x − 2x − 1 = 4x2 − 1