Although a Pentagon only has one more side/edge than a standard square or rectangle.
Establishing the area of a regular Pentagon, is slightly more involved and complex in comparison.
If we have a regular Pentagon as pictured below.
The area can be worked out with a general formula for the area of a Pentagon.
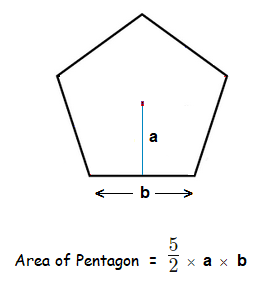
Though more involved work generally involves working out the value of a first.
The bulk of this page shows where the formula for the area of a Pentagon comes from, and how to establish the value of a.
But if you’re simply looking to find an example on its own where the value of a is already known.
There is an example at the base of this page, which you can scroll straight to if you wish.
Derive Formula for Area of Pentagon
For a regular Pentagon, all exterior angles add up to 360°.
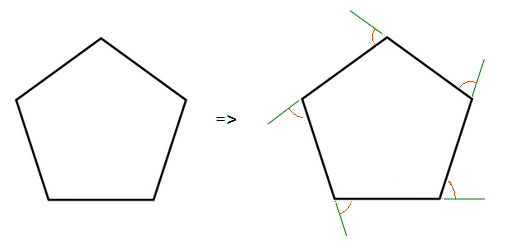
As can be seen, there are 5 exterior angles with a Pentagon, and they are all of equal size.
Regardless of how large or small the Pentagon is.
The size of 1 exterior angle is. \frac{360}{5} = 72°
This can tell us what size the interior angles of the Pentagon are.
As it’s the case that one side of a straight line is of size, 180°.
The size of an interior angle can be given by. 180° − 72° = 108°
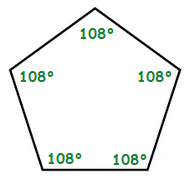
Now if we leave the size of the interior angles to the side for a brief moment.
A regular Pentagon can be divided up into 5 equal sized triangles.
By drawing straight lines from the central point of the Pentagon, to the corners.
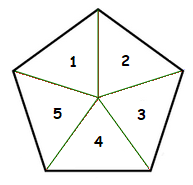
As all the inside triangles are the same size, if we can find the area of just 1 of the triangles.
We can then find the area of a whole Pentagon, by multiplying the triangle area by 5.
In order to find the area of 1 of the triangles though, some more information is required than what we have thus far.
Each of the straight lines from the central point of the Pentagon to the corners, actually cuts each corner in half evenly.
Now as each interior angle is 108°.
The size of each angle on each side of the straight lines can be given by. \frac{108\degree}{2} = 54°.
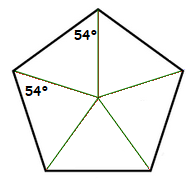
The next thing to realize, is that each of the 5 triangles inside the Pentagon, can themselves be divided into 2 smaller right angle triangles.
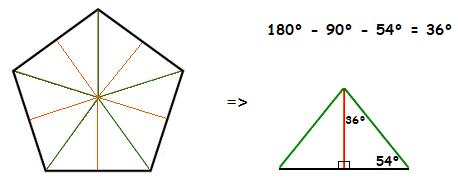
Each one of these 10 new smaller triangles in the Pentagon, is a right angle triangle.
A right angle triangle that we happen to know the size of all the interior angles.
Now lets’ see how all this helps with working out the area of a specific regular Pentagon, where the sides/edges are all 8cm in length.
Formula for Area of Pentagon Example
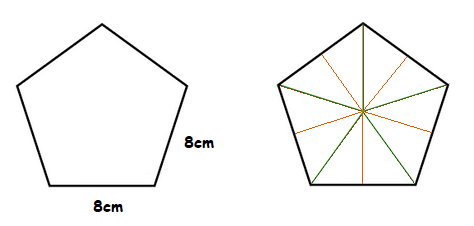
Like any standard regular Pentagon, this Pentagon can be divided up into smaller triangles as seen earlier.
The angles of each smaller right angle triangle, are always the same size, no matter how big or small the Pentagon itself is.
But the length of the sides of the triangles can differ.
With this Pentagon, the base of one of the smaller right angle triangles will be 4cm, half of an entire 8cm edge.
Triangles in Pentagon:
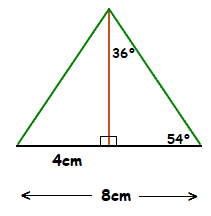
As the area of a triangle is given by, \frac{1}{2} × BASE × HEIGHT.
Here we just need to work out the length of the height, which is the red line.
As we will then be able to work out the area of the whole larger triangle with base 8cm.
Then, this triangle area being multiplied by 5, will result in the area of the whole Pentagon.
Looking at just one of the right angle triangles, we can use some Trigonometry to work out the size of the red line, the height.
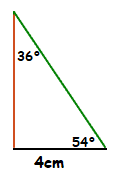
tan = \frac{\tt{opposite}}{\tt{adjacent}}
For the angle 54° here, the adjacent side is 4cm, and the opposite side is the height.
tan( 54° ) = \frac{\tt{height}}{\tt{4}} ( × 4 )
4 × tan(54°) = height , 5.5 = height
Now that we know the values of both the base and the height of the larger triangle, we are able to work out the area.
AREA = \frac{\bf{1}}{\bf{2}} × 8 × 5.5 = 22cm2
So for the area of the entire Pentagon, as there are 5 larger triangles inside, we just multiply 22cm2 by 5.
AREA OF PENTAGON = 22cm2 × 5 = 110cm2
It turns out all we actually needed to establish the area of one of the 5 triangles, was the length of the red height line, along with the length of a side/edge of the Pentagon.
This red line we’ve been using for the height of the triangles. From the central point of an edge/side, to the central point of the whole Pentagon, isn’t just the line for the height of the triangles.
It’s also a specific straight line that is called the apothem.
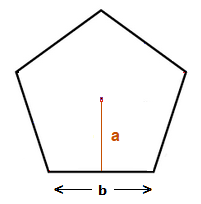
Looking at what we’ve seen on this page.
Area of a Pentagon was: ( AREA of 1 triangle ) × 5
With:
AREA of 1 triangle = \frac{1}{2} × a × b,
So: ( \frac{1}{2} × a × b ) × 5 = \frac{5}{2}ab
This is how the formula for area of Pentagon comes about, which we can use provided we know the values of a and b.
Example
1.1
Find the area of a regular Pentagon which has the following measurements.
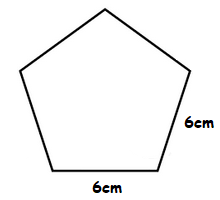
Solution
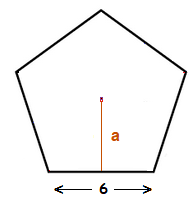
For \frac{\bf{5}}{\bf{2}}ab,
b = 6 , just need to establish the value of a.
The same approach as before with an appropriate right angle triangle can be used.
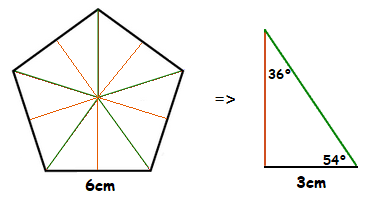
tan( 54° ) = \frac{\bf{a}}{\bf{3}} ( × 3 )
3 × tan( 54° ) = a
4.13 = a
Now: \frac{\bf{5}}{\bf{2}}ab = \frac{\bf{5}}{\bf{2}} × 4.13 × 6 = 61.95
The area of the Pentagon is 61.95cm2.