This page will show how to convert between fractions and mixed numbers when the fractions are improper, and the overall value of the fraction is larger than 1.
Being able to carry out these conversions, especially mixed number to a fraction, can be useful when dealing with a range of fractions sums.
Convert Mixed Number to a Fraction
We could have a mixed number such as 3\bf{\frac{4}{5}}.
We may wish to convert this to an entire fraction, an improper fraction.
This is something that can be done following 3 steps.
1) Multiply the whole number part with the denominator of the fraction part.
2) Add the result of this multiplication with the numerator of the fraction part.
The result of this addition will be the numerator of the new fraction we’re creating.
3) To complete the conversion, the original denominator in the mixed number will also be the denominator of our new fraction.
Examples
1.1
Convert 3\bf{\frac{4}{5}} to a mixed fraction.
Solution
Let’s look at our mixed fraction from above, 3\bf{\frac{4}{5}}.
3 × 5 = 15
15 + 4 = 19 The new fraction we have now is \bf{\frac{19}{5}}.
Or instead, we can also carry out the steps as the following sums, which can be a bit and simpler and faster.
3\bf{\frac{4}{5}} = \boldsymbol{\frac{3 \space \times \space 5 \space + \space 4}{5}} = \boldsymbol{\frac{15 \space + \space 4}{5}} = \bf{\frac{19}{5}}
Thus {\frac{19}{5}} is the improper fraction form of 3{\frac{4}{5}}, they represent the same overall value.
1.2
Convert the mixed number 4\bf{\frac{2}{9}} to a standard fraction.
Solution
4\bf{\frac{2}{9}} = \boldsymbol{\frac{4 \space \times \space 9 \space + \space 2}{9}} = \boldsymbol{\frac{36 \space + \space 2}{9}} = \bf{\frac{38}{9}}
1.3
Convert – 2\bf{\frac{3}{4}} to a standard fraction.
Solution
When converting a negative mixed number to a fraction, a good way to proceed is to simply carry out the sums as usual, but keeping a minus sign at the side for the fraction at the end.
–2\bf{\frac{3}{4}} = – ( \boldsymbol{\frac{2 \space \times \space 4 \space + \space 3}{4}} ) = – ( \boldsymbol{\frac{8 \space + \space 3}{4}} ) = –\bf{\frac{11}{4}}
Summary
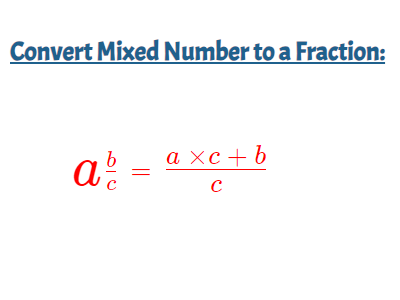
Fractions and Mixed Numbers,
Convert a Fraction to a Mixed Number
We can also work the other way, an improper fraction can be converted to a mixed number.
The steps to be taken are a little different, but again fairly straightforward to learn.
We can look at the fraction \bf{\frac{16}{5}} for a conversion.
1) Carry out the division of 16 divided by 5. 16 ÷ 5 = 3 remainder 1
2) From this division result, the main number 5 will be the whole number part of the new mixed number. 5
3) The remainder from the division will be the numerator of the fraction part, above the original denominator. 3\bf{\frac{1}{5}}
Examples
2.1
Convert the improper fraction \bf{\frac{19}{4}} to a mixed number.
Solution
19 ÷ 4 = 4 remainder 4, giving us 4\bf{\frac{3}{4}} as the mixed number form.
2.2
Convert –\bf{\frac{11}{2}} to a mixed number.
Solution
The fraction to be converted being negative doesn’t affect the steps, the process is just the same we just remember the minus sign.
–11 ÷ 2 = –5 remainder 1 , resulting in – 5\bf{\frac{1}{2}} as the mixed number form here.
- Home ›
- Fractions and Decimals › Mixed Numbers and Fractions