Skip to content

Multiplication of Fractions Examples



Dealing with multiplication of fractions examples usually isn’t terribly difficult. But it is something that one needs to pay attention to when doing.



Multiply Fraction by a Number

The most basic multiplication sums involving fractions are when a whole number multiplys a fraction, such as:

2 × \frac{2}{3}

When this is the case, you just multiply the numerator on the top line by the whole number.

a)     2 × \frac{2}{3}   =   \frac{2 \space \times \space 2}{3}   =   \frac{8}{3}

b)     3 × \frac{5}{4}   =   \frac{3 \space \times \space 5}{4}   =   \frac{15}{4}

c)     –4 × \frac{1}{5}   =   \frac{{\text{-}}4 \space \times \space 1}{5}   =   –\frac{4}{5}

d)     2 × –\frac{5}{3}   =   –\frac{2 \space \times \space 5}{3}   =   –\frac{10}{3}




Multiply a Fraction by a Fraction

The general approach with multiplying fractions together is the same as when dealing with multiplication of fractions examples involving whole numbers.
But the denominators on the bottom line will also be multiplied together.


Examples



1.1

\frac{1}{2} × \frac{5}{6}   =   \frac{1 \space \times \space 5}{2 \space \times \space 6}   =   \frac{5}{12}


1.2

\frac{1}{3} × \frac{3}{5}   =   \frac{1 \space \times \space 3}{4 \space \times \space 5}   =   \frac{3}{20}


1.3

\frac{8}{5} × \frac{3}{4}   =   \frac{8 \space \times \space 3}{5 \space \times \space 4}   =   \frac{24}{20}   =   \frac{6}{5}



Summary

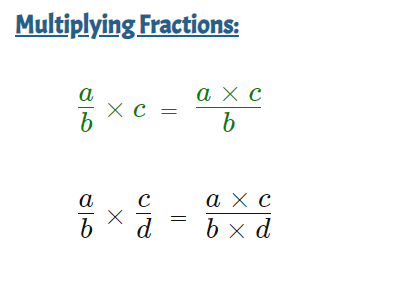
General rule for the multiplication of fractions.


Multiplication of Fractions Examples
Mixed Numbers

In cases where fractions are presented as mixed numbers, also called mixed fractions, we generally want to put them into improper fraction form first before multiplying.
Then we can then write the answer back as a mixed fraction if we can.

More information on converting between fractions and mixed numbers can be seen here here.



Examples



2.1
1\bf{\frac{3}{4}} × 1\bf{\frac{5}{7}}

=   ( \bf{\frac{1 \space \times \space 4 \space + \space 3}{4}} )  ×  ( \bf{\frac{1 \space \times \space 7 \space + \space 5}{7}} )   =   \bf{\frac{7}{4}} × \bf{\frac{12}{7}}   =   \bf{\frac{84}{28}}   =   3


2.2
2\bf{\frac{1}{4}} × 1\bf{\frac{1}{2}}

=   ( \bf{\frac{2 \space \times \space 4 \space + \space 1}{4}} )  ×  ( \bf{\frac{1 \space \times \space 2 \space + \space 1}{2}} )   =   \bf{\frac{9}{4}} × \bf{\frac{3}{2}}   =   \bf{\frac{27}{8}}   =   3\bf{\frac{3}{8}}


2.3
–3\bf{\frac{2}{3}} × 2\bf{\frac{1}{3}}

=   –( \bf{\frac{3 \space \times \space 3 \space + \space 2}{3}} )  ×  ( \bf{\frac{2 \space \times \space 3 \space + \space 1}{3}} )   =   –\bf{\frac{11}{3}} × \bf{\frac{7}{3}}   =   –\bf{\frac{77}{9}}   =   –8\bf{\frac{5}{9}}






  1. Home
    2.  ›
  2. Fractions and Decimals
    3. › Fractions Multiplication


Return to TOP of page