Flat 2D polygon shapes in Math, will create a certain number of angles with the edges and corners of the shape.
These will be angles that are both inside and outside the shape, we refer to them as interior and exterior angles.
Interior angles were covered on the angles in triangles and common shapes page.
Shapes and Exterior Angles
Different to interior angles, exterior angles are the angles that are formed on the outside of a polygon shape.
An exterior angle is formed between one side of the shape itself, and another straight line extending from the following side.
Below is a standard triangle, with exterior angles drawn in red.
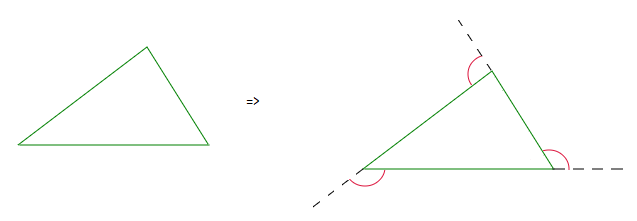
It turns out the interior and exterior angle at each point/vertex of a polygon shape sum up to 180°, they are supplementary angles.
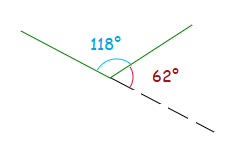
118° + 62° = 180°
Polygons and Exterior Angles
For a regular polygon, that is a polygon where all sides are the same length, and all inside angles the same size, all exterior angles add up to 360°.So for a regular polygon with n number of sides and angles.
To find the value of an exterior angle, you can do the sum:
\frac{360\degree}{n}
Example
1.1
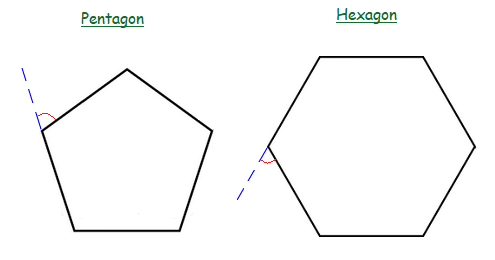
Pentagon External Angle = \tt{\frac{360\degree}{5}} = 72°
Hexagon External Angle = \tt{\frac{360\degree}{6}} = 60°
Triangle Exterior Angle Theorem
With shapes and exterior angles, when it comes to exterior angles involving triangles specifically.
There is a theorem that is referred to as the “Exterior Angle Theorem”.
This theorem states that the exterior angle of a triangle is equal to the sum of the two opposite interior angles which are inside the triangle.
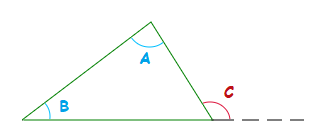
In the above triangle: Angle C = A + B
This holds true because of the fact that all three interior angles of a triangle add up to 180°.
Along with the fact that supplementary angles along a straight line also add up to 180°.
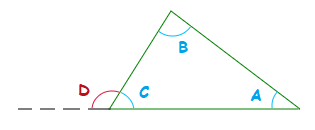
For the angles in the above triangle.
A + B + C = 180° and C + D = 180°So A + B + C = C + D.
=> A + B + C − C = C + D − C
=> A + B = D
Examples
2.1
What is the size of angle S ?
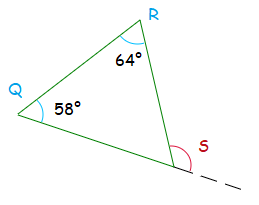
Solution
Angle S = 58° + 64° = 122°
2.2
What is the size of angles D and E ?
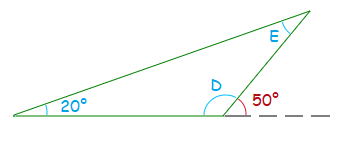
Solution
Angle E + 20° = 50°
Angle E = 50° − 20° = 30°
Angle D is Supplementary with 50°,
Angle D = 180° − 50° = 130°.