Before focusing primarily on vertically opposite angles, it’s very useful to first understand what complementary and supplementary angles are.
Complementary Angles
Complementary angles are 2 angles that when they are added together they sum up to 90°.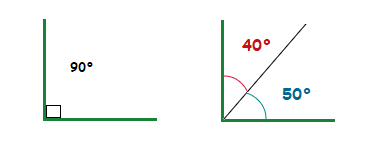
40° and 50° are complementary to each other as angles, as they add up to 90°.
The 2 angles concerned don’t always have to be adjacent, where the angles share a common point/vertex along with a common side between them.
As well as being presented along side each other. Complementary and Supplementary angles can also be apart from each other, thus sharing no point/vertex or side.
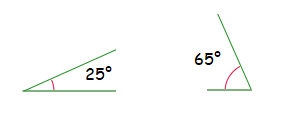
25° and 65° are complementary to one another also. 25° + 65° = 90
Example
1.1
What angle is complementary to 62°?
Solution
90° − 62° = 28° , 28° + 62° = 90°
The angle 28° is complementary with the angle 62°.
Supplementary Angles
The concept of supplementary angles is fairly similar to complementary angles.
Supplementary angles are angles that when they are added together they sum up to 180°.

110° and 70° are angles that are supplementary. 110° + 70° = 180°
Like with the case of complimentary angles, supplementary angles don’t have to be right next to each other, but at times they can be.
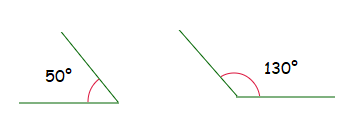
130° and 50° are supplementary. 130 + 50° = 180°
Example
2.1
What angle is supplementary with 116°?
Solution
180° − 116° = 64° , 116° + 64° = 180°
The angle 64° is supplementary with the angle 116°.
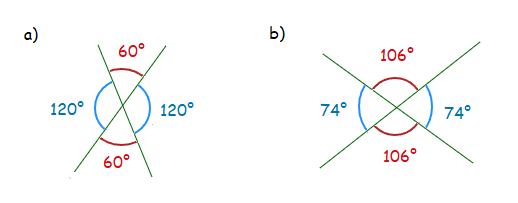
Vertically Opposite Angles
Vertically opposite angles, which can also known as vertical angles.
Are 2 angles of the same size, that are formed between opposite sides of 2 straight lines which intersect.
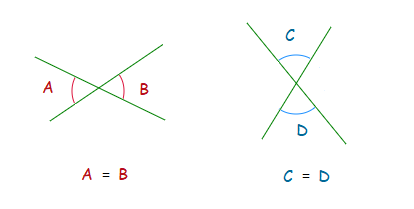
Vertical Angles Theorem
This theorem happens to be a type of proof with regards to the value of angles that are vertically opposite.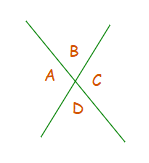
In the diagram above angles A and B are supplementary with each other, thus add up to 180°.
A + B = 180°
Angles B and C are also angles that are supplementary with each other.
B + C = 180°
A + B = B + C
Now from here, using a bit of Algebra.
A = B + C − B => A = C
The same approach can be used for the equality of angles B and D.