Multiples of Numbers
What are Lowest Common Multiples

Multiples of numbers, are the result of multiplying given numbers by integers.

Integers  =  { …. , -3 , -2 , -1 , 0 , 1 , 2 , 3 , …. }

Multiples Intro

Let’s consider an example of the number  6.

6 × 0  =  0     ,     6 × 1  =  6     ,     6 × 2  =  12     ,     6 × 3  =  18     ,     6 × -1  =  -6


The numbers   0, 6, 12, 18   and   –6   are all multiples of the number  8.

They each are the result of multiplying  6  by another number.



Fractions and Multiples

Fractions can also have multiples just like whole numbers.

{\large{\frac{1}{2}}} \times 0 \space = \space 0     ,     {\large{\frac{1}{2}}} \times 1 \space = \space {\large{\frac{1}{2}}}     ,     {\large{\frac{1}{2}}} \times 2 \space = \space 1     ,     {\large{\frac{1}{2}}} \times 3 \space = \space {\large{\frac{3}{2}}}


All the answers above, are multiples of  \frac{1}{2}.

Multiples of Numbers, Common Multiples

With multiples of numbers, a common multiple is a number that happens to be a multiple of  2  or more other numbers.

We can list some multiples of  2.     =>     2 , 4 , 6 , 8 , 10 , 12

Some multiples of  6.     =>     6 , 12 , 18

It can be seen that  6  and  12  are common multiples of  2  and  6.

What are Lowest Common Multiples,
Lowest Common Multiple

What are lowest common multiples?

In Math the lowest common multiple of a pair of positive numbers or a larger group of positive numbers, is the smallest positive number that is a multiple of each number.


Examples


1.1

Find the lowest common multiple of the numbers  5  and  6.

Solution

One effective method is to list out the multiples of each number, and looking for the smallest shared multiple in both lists.

5   =>   { 5 , 10 , 15 , 20 , 25 , 30 , 35 , 40 , 45 , 50 , …. }

6   =>   { 6 , 12 , 18 , 24 , 30 , 36 , 42 , 48 , 54 , 60 , …. }

From the lists it can be seen that  30  is the lowest common multiple of  5  and  6.



1.2

Find the lowest common multiple of  3,  6  and  14.

Solution

3   =>   { 3 , 6 , 9 , 12 , 15 , 18 , 21 , 24 , 27 , 30 , 33 , 36 , 39 , 42 , 45 , … }

6   =>   { 6 , 12 , 18 , 24 , 30 , 36 , 42 , 48 , 54 , … }

14   =>   { 14 , 28 , 42 , 58 , … }

42  is the lowest common multiple of  3, 6  and  14.



1.3

There is another approach also than can be used.

Firstly, draw up an appropriate table and begin dividing each given number exactly, starting with a divisor of  2.

Then keep dividing each result we get, increasing the value of the divisor where necessary.

Until we eventually obtain a result of  1,  with no more exact division to be carried out.

We can look at the case of the lowest common multiple of  5  and  21.

These numbers that were used in the divisions, multiplied together will give the lowest common multiple of both numbers.

3 × 5 × 7  =  105

We can see this by drawing up a list of the factors of  5  and  9.

5   =>   { 5 , 10 , 15 , 20 , ……. , 90 , 95 , 100 , 105 , 110 , … }
21   =>   { 21 , 42 , 63 , 84 , 105 , 110 , … }




1.4

Find the lowest common multiple of  40  and  175.

Solution

Here we can use the table and division method.

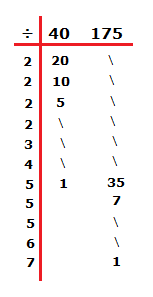
2  was used in the division three times,  5  two times and  7  one time.

2 × 2 × 2 × 5 × 5 × 57  =  1’400

1’400  is the lowest common multiple of  40  and  170.




1.5

Find the lowest common multiple of  4,  6  and  9.

Solution

We can also find the lowest common multiple of more than just two numbers.
The table and division method still works the same way.

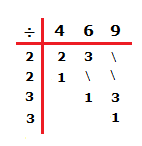
2  was used in the division two times, and  3  was used two times.

2 × 2 × 3 × 3  =  36

36  is the lowest common multiple of  4,  6  and  9.

---

1. Home
 ›
2. Arithmetic/Numbers
› Multiples, Lowest Common Multiple

Return to TOP of page